Simulation von Kreis- und Ellipsenbahnen um die Erde mit Visualisierung in Python. Enthält Hohmann-Transferellipse sowie Δv1/Δv2/Δv_total und Transferzeit.
Screenshots
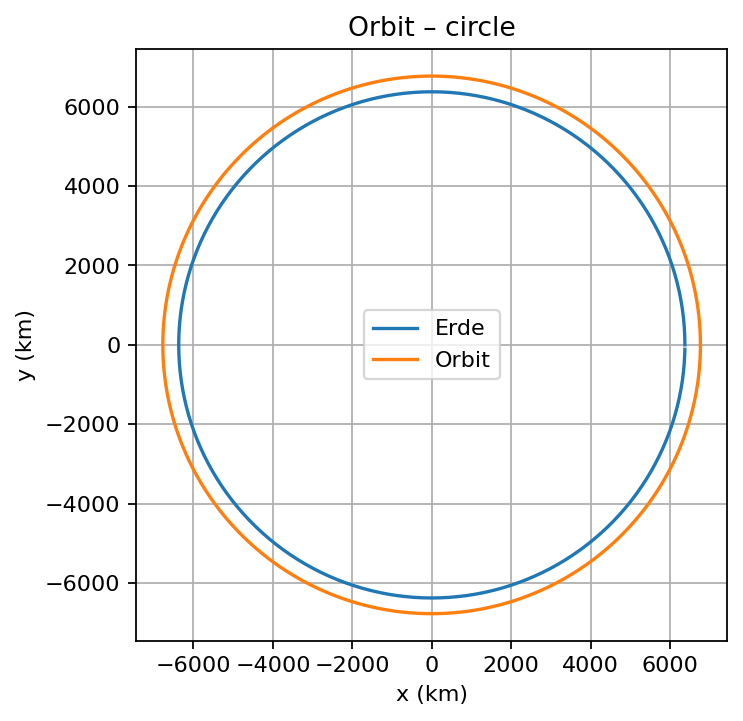
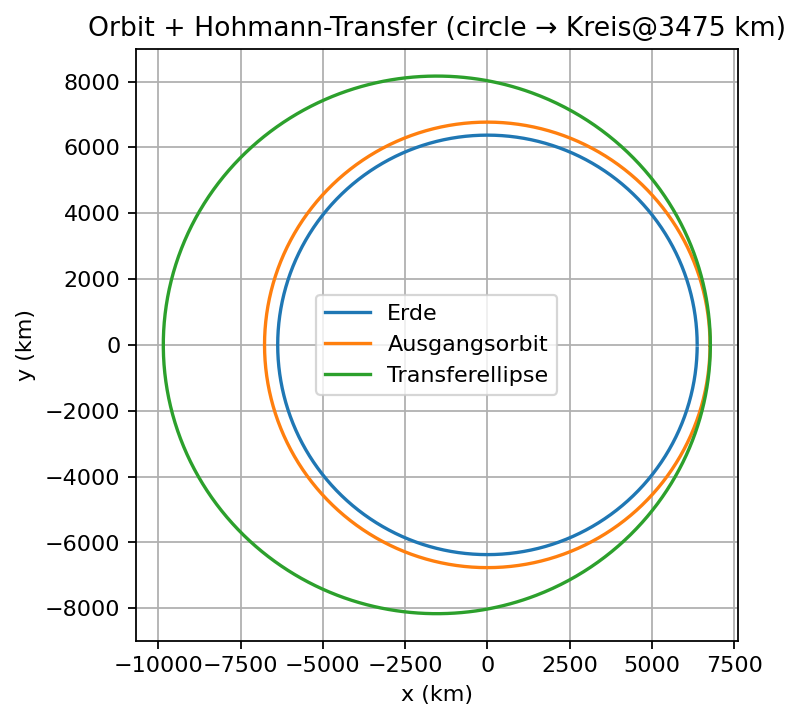
Beispielausgabe
| Höhe | Geschwindigkeit | Umlaufzeit | Orbit-Typ |
|---|---|---|---|
| 400 km | 7.67 km/s | 92 min | Kreisbahn |
| 35.786 km | 3.07 km/s | 1429 min | GEO-Kreisbahn |
Dieses Projekt zeigt, wie man mit Python grundlegende Himmelsmechanik berechnen kann. Typische Größen wie Kreisgeschwindigkeit, Fluchtgeschwindigkeit oder Umlaufzeit werden automatisch berechnet und anschaulich visualisiert.
Code-Beispiele
Orbit berechnen
from orbit_logic import compute_orbit_at_radius
Beispiel: LEO (400 km Höhe, 7.67 km/s)
result = compute_orbit_at_radius(400, 7.67)
print(result["type"]) -> "circle"
print(result["period_min"]) -> Umlaufzeit in Minuten
Mit compute_orbit_at_radius wird aus Höhe + Geschwindigkeit der Orbit bestimmt.
Das Ergebnis enthält den Typ (Kreis, Ellipse oder Fluchtbahn), Perigäum, Apogäum
und Umlaufzeit.
Hohmann-Transfer berechnen
from orbit_core import hohmann_delta_v, hohmann_transfer_time
from constant import MU, R_EARTH
from units import km_to_m
r1 = R_EARTH + km_to_m(400) Start in LEO
r2 = R_EARTH + km_to_m(35786) Ziel: GEO
dv1, dv2, dv_total = hohmann_delta_v(MU, r1, r2)
t = hohmann_transfer_time(MU, r1, r2)
print(dv1, dv2, dv_total, t)
Damit lassen sich die Δv-Werte für einen Hohmann-Transfer sowie die Transferzeit zwischen zwei Kreisbahnen berechnen.
Kurzinfo
- Orbit-Report: Perigäum, Apogäum, Umlaufzeit, Referenz-Geschwindigkeiten
- Hohmann-Transfer: Δv1, Δv2, Δv_total, Transferzeit
- Matplotlib-Plots, Export in
data/ - Saubere Modulstruktur (core/logic/visualize/cli)